什么是最小二乘法?
最小二乘法是一种数学回归分析的形式,用于确定一组数据的最佳拟合线,为数据点之间的关系提供一个直观的展示。每一个数据点都代表了一个已知自变量和一个未知因变量之间的关系。
- 最小二乘法是一种统计程序,通过最小化各点与所绘曲线的偏移或残差之和,为一组数据点找到最佳拟合
- 最小二乘法的回归是用来预测因变量的行为
- 最小二乘法为所研究的数据点之间的最佳拟合线的位置提供了总体理由
这种回归分析方法始于一组要在X轴和Y轴图形上绘制的数据点。使用最小二乘法的分析员将产生一条最佳拟合线,解释自变量和因变量之间的潜在关系。
最小二乘法为最佳拟合线在所研究的数据点中的位置提供了总体理由。这种方法最常见的应用,有时被称为 “线性 “或 “普通”,目的是创建一条直线,使相关方程的结果产生的误差平方之和最小,如观察值和预期值的差异导致的平方残差,基于该模型。
最佳拟合线方程
由最小二乘法确定的最佳拟合线有一个方程,讲述了数据点之间的关系。最佳拟合线方程可以由计算机软件模型确定,其中包括分析的输出摘要,其中的系数和输出摘要解释了被测试变量的依赖性。
最小二乘法的例子
分析师希望测试一家公司的股票收益与该股票所属的指数收益之间的关系。在这个例子中,分析家试图测试股票收益对指数收益的依赖性。
为了达到这个目的,所有的回报都被绘制在一个图表上。指数收益被指定为自变量,而股票收益是因变量。最佳拟合线为分析员提供了解释依赖程度的系数。
为了说明这一点,请考虑一个投资者考虑是否投资于一家金矿公司的案例。该投资者可能希望知道该公司的股票价格对黄金市场价格的变化有多敏感。为了研究这个问题,投资者可以使用最小二乘法,在散点图上追踪这两个变量在一段时间内的关系。这种分析可以帮助投资者预测在任何特定的黄金价格上升或下降的情况下,股票价格可能上升或下降的程度。

Matlab作业代做-最小二乘模型案例
利用最小二乘原理,编写求取模型参数k_12 、k_13 、k_14 、k_15 、k_23 、k_24 、k_25 、k_34的matlab程序。其它均为已知。
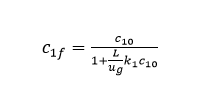
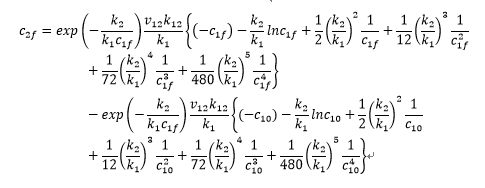
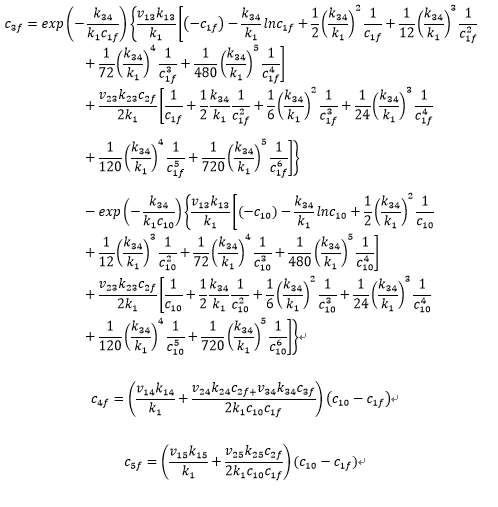
上述式子中,k_1=k_12+k_13+k_14+k_15 k_2=k_23+k_24+k_25
v_ij=M_i/M_j c_if=y_i/M_i
式中ci0、cif —— 反应前入口浓度、反应后出口浓度,mol/kg;u_g —— 油气在反应器内的流速,m/s;k_ij —— I集总生成J集总的速率常数; v_ij —— I集总生成J集总的化学计量系数;y_i —— I集总的质量产率,wt%;Mi —— I集总的摩尔质量,kg/mol.